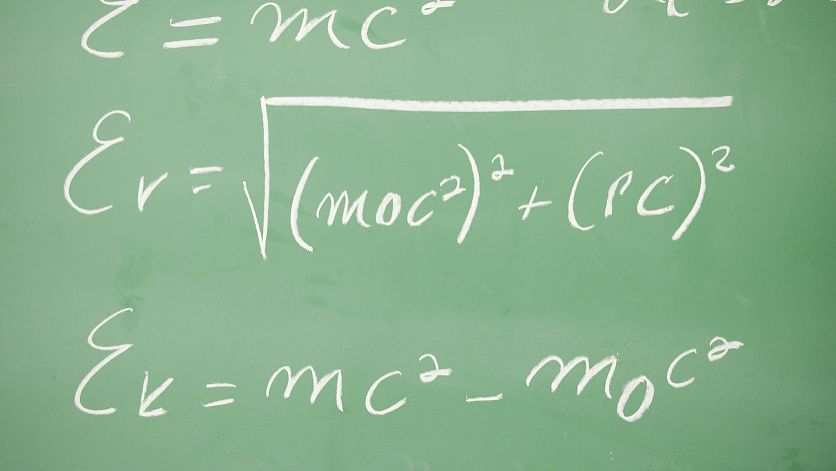似乎很多人知道这个方程的解可以写成这样。。

这个表达式已经经过很多软件的验证了。。稳稳的是对的
说真的我第一眼看到这个的时候简直吓尿了。。虽然是很久之前看到的了,但直到今天我才知道这是怎么算出来的。。
起因是上午吧里有人问了一个和这个相关的问题,又勾起了我的兴趣。。加上比较闲我就又去查了查资料。。结果运气不错让我找到了解法233
对于t*sinE=E-M这样的方程,在给定t 和M的值之后是可以解析的求出E的,方法见下面这篇文献
链接:http://pan.baidu.com/s/1gfxevPD 密码:jykn
之后考虑方程cosx=x,令x=y-π/2可以得到siny=y-π/2,按照文献中的方法求解即可
据说数吧在今天成立了汉化组,他们似乎对汉化上面这篇文献跃跃欲试,应该会在近期放出汉化版,让我们期待一下吧(怕不是一口毒奶 )
)
上午勾起我兴趣的那贴莫名其妙的被删了(似乎是锑度干的,mdzz),导致很多人没有看到。。而这一部分我又觉得挺有意思,值得分享一下。。所以才开了这一贴。。绝对不是为了水晶燕
------虽然我只是一个2级萌新,但请相信我,我水到7级就不会再水了。
PS:别跟我说我已经9级了,我懒得改

这个表达式已经经过很多软件的验证了。。稳稳的是对的
说真的我第一眼看到这个的时候简直吓尿了。。虽然是很久之前看到的了,但直到今天我才知道这是怎么算出来的。。
起因是上午吧里有人问了一个和这个相关的问题,又勾起了我的兴趣。。加上比较闲我就又去查了查资料。。结果运气不错让我找到了解法233
对于t*sinE=E-M这样的方程,在给定t 和M的值之后是可以解析的求出E的,方法见下面这篇文献
链接:http://pan.baidu.com/s/1gfxevPD 密码:jykn
之后考虑方程cosx=x,令x=y-π/2可以得到siny=y-π/2,按照文献中的方法求解即可
据说数吧在今天成立了汉化组,他们似乎对汉化上面这篇文献跃跃欲试,应该会在近期放出汉化版,让我们期待一下吧(怕不是一口毒奶
上午勾起我兴趣的那贴莫名其妙的被删了(似乎是锑度干的,mdzz),导致很多人没有看到。。而这一部分我又觉得挺有意思,值得分享一下。。所以才开了这一贴。。绝对不是为了水晶燕
------虽然我只是一个2级萌新,但请相信我,我水到7级就不会再水了。
PS:别跟我说我已经9级了,我懒得改


 爱尔奎特
爱尔奎特
 第四人称
第四人称